半導体電バイスの電気的特性の評価はいくつかの手法があります。今回はその中の一つであるTLM法についてご紹介します。
TLM法とは?
TLM法(Transfer length method法)とはチャネルのシート抵抗と電極/チャネル界面の接触抵抗を求めることが出来る方法になります。以下に示すように様々な間隔で電極を並べます。この時IV測定によって算出した抵抗値から接触(コンタクト)抵抗とシート抵抗を計算することが出来ます。
材料の抵抗率を知りたい、デバイスのコンタクト抵抗を知りたい。。
そんな時は是非今日扱うTLM法を実践してみてください!
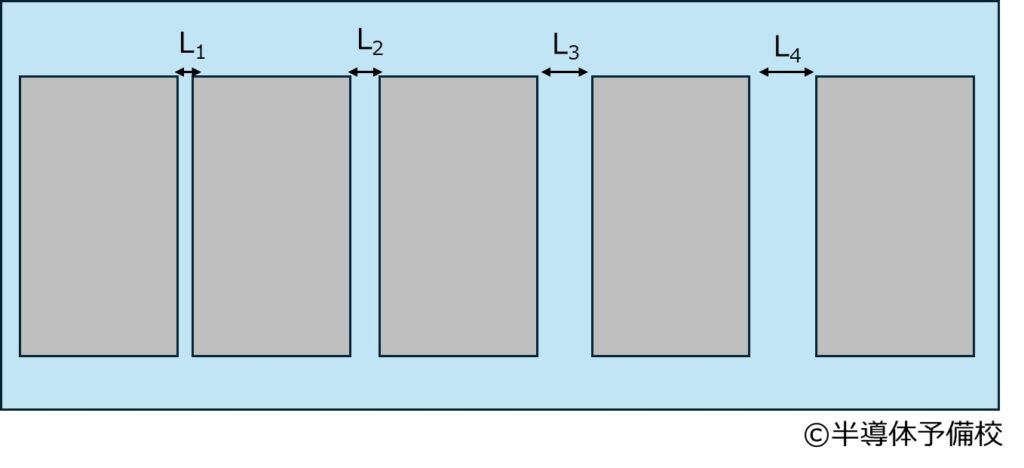
TLM法の原理
金属の抵抗値は
$$R=ρ\frac{L}{S}$$
で計算されます。つまり長さが伸びるにつれ抵抗値が増えます。
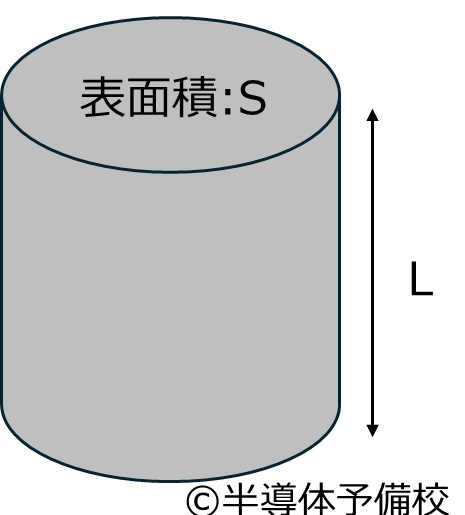
TLM法はこの性質を利用します。
下記のようなシートがあるとして、長さLを変えるとそれに比例して抵抗値が変わることが分かります。
**画像挿入**
接触抵抗は電極/シートの界面で生じる固定値なので定数です。
つまり
$$R_T=R_f(L)+2R_c$$
のという式で計算することが出来ます。なぜRcの部分に2があるかというと電流を流すときに電極は2つあるため(+と-の極)、接触抵抗が生じる部分が2か所存在するからです。

実際グラフにしてみると以下のようになり、傾きからシート抵抗・切片から接触抵抗を求めることが可能です。

その① 実際に抵抗率を求める方法
実際にシート抵抗・コンタクト抵抗を求める使い方もありますが、大体は「シート抵抗から抵抗率を出したい」・「面積当たりの接触抵抗を知りたい」といったニーズが多いと思います。
このような縦:W [um] 横:d [um]の電極と抵抗率ρc [Ω・m^2] 膜厚 t [um]のチャネルを想定します。
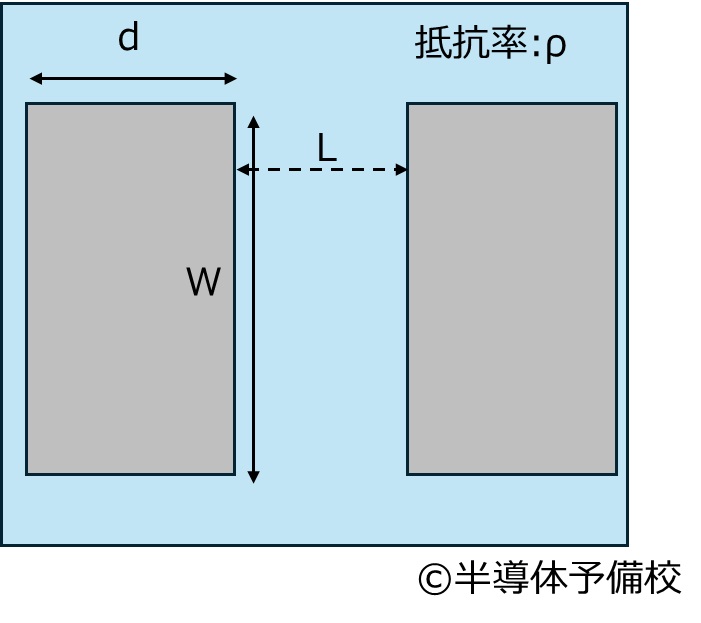
チャネル部の抵抗は
$$R=ρ \frac{L}{t\times W}$$
ここでシート抵抗という概念を「単位表面積当たりの抵抗」と定義して導入します。
$$Rsh=\frac{ρ}{t}$$
$$R=R_sh \frac{L}{W}$$
電極の縦長さWは既知なのでTLMの結果から出た直線の傾き aからRshを求めることが出来ます。
その② 実際に固有接触抵抗を求める方法
TLM法では切片がコンタクト抵抗の2倍になるとお伝えしました。実際に研究等で求めたいのは「その電極/チャネルのコンタクト抵抗が面積当たりにどのくらいなのか?」ということだと思います。
コンタクト抵抗は何か?ということから戻って考えましょう。電流は下記のように電気力線が伸びている領域を流れます。つまり電極の下側も厳密には電気力線が伸びています。この部分がコンタクト抵抗の正体です。

この電気力線が伸びた距離のことを遷移長(Lt)とよびます。LtはTLM法の直線におけるx切片から考えることが出来ます。(x切片は-2Ltとなります。)
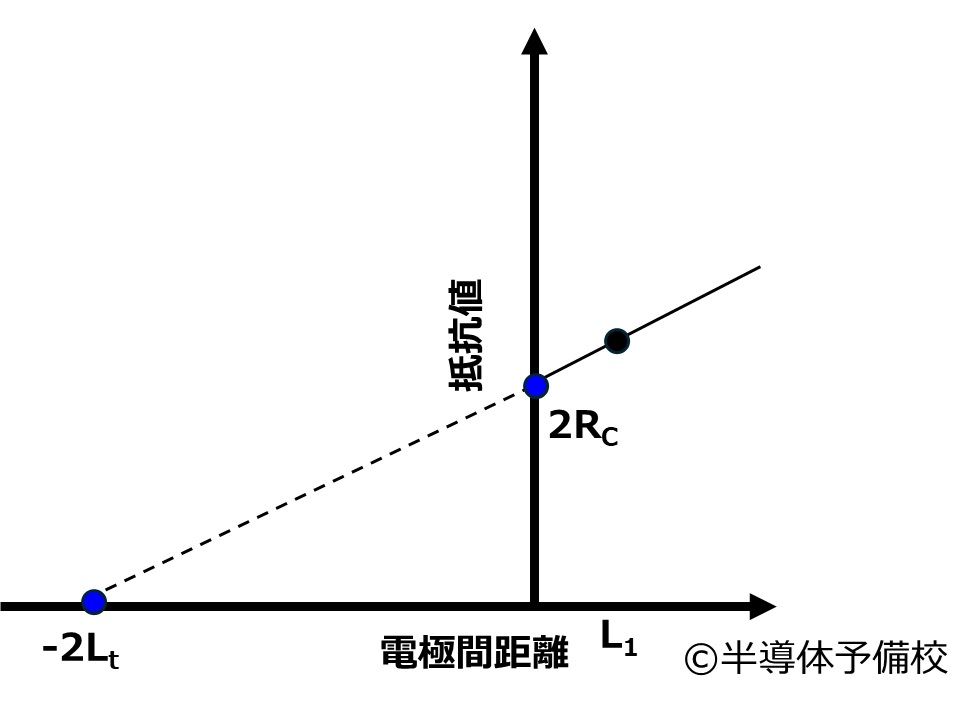
ここで電極下でのシート抵抗をRskとするとコンタクト抵抗は
$$R_c=R_{SK} \times\frac{L_t}{W}$$
と求めることが出来ます。
もし仮にチャネルが半導体であり、電極/半導体界面がきれいに分かれている場合、電極下で発生する抵抗はチャネルのシート抵抗と考えることができRsk=Rshとなります。d>>>Ltの場合
固有接触抵抗ρcは
$$\frac{ρ_c}{W \times L_t} =R_c$$
より
$$ρ_c =R_c\times (W\times L_t)=R_{sk}\times {L_t}^2$$
となり求めることが出来ます!
C-TLM法とは!?
先ほどの長方形パターンを測定することで、コンタクト抵抗・シート抵抗を求めることが出来ます。(原理的には。。。。)ただし実際には電極間距離に対して十分なWを稼がなければ、矩形部からの電気力線の染み出しが無視できず正確な測定結果を得ることが難しくなります。
そこで円形のパターンを用いることで、矩形をなくしより正確な測定を試みる方法があります。それがC-TLM法です。
先ほどと原理は同様で、電極間距離を変えた円形パターンを複数つくり電圧をプロットすることで傾きと切片からシート抵抗とコンタクト抵抗を出すことが可能です。
長方形のパターンと異なり少し計算が複雑です。
まず先ほどはWが一定でしたが、今回内円と外円の半径が異なります。
電極間距離:d [um],内円半径r1 : a [um],外円半径r2 : b[um]とすると。
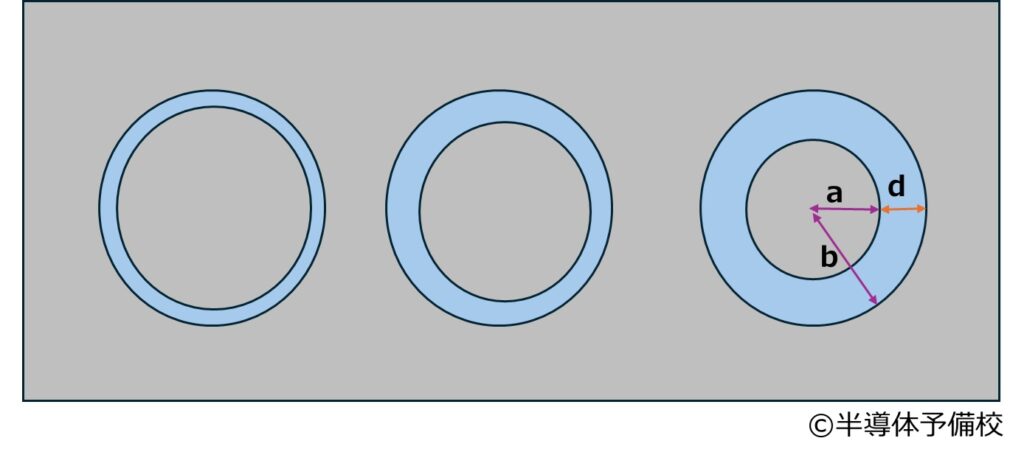
チャネルの面積は
$$S = π\times(b^2-a^2)=π\times(b+a)(b-a)=π\times (b+a) \times d $$
とdに比例することは変わりませんが、面積は内円と外円の大きさも影響してきます。
抵抗Rは下記の式で計算可能です。
$$R=\frac{R_{sh}}{2π}ln(\frac{b}{a})+\frac{ρ_c}{2π L_s}(\frac{1}{a}+\frac{1}{b})$$
1項目はシート抵抗,2項目はコンタクト抵抗の項になります。
この式からC-TLM法の場合横軸はb/aの対数を横軸にした時の傾きからシート抵抗が求められることが分かります。傾きをMとすると
$$Rsh=2π\times M$$
また遷移長は下記のような定義なので
$$L_s=\sqrt{\frac{ρ_c}{R_{sh}}}$$
$$ρ_c=R_{sh}{L_s}^2$$
また切片からコンタクト抵抗もわかります!
切片をIとすると、
$$I=\frac{ρ_c}{2π L_s}(\frac{1}{a}+\frac{1}{b}$$
ですね。 ρcを代入すると、、、
$$I=\frac{R_{sh}{L_s}^2}{2π L_s}(\frac{1}{a}+\frac{1}{b}$$
計算すると
$$L_s=\frac{2πI}{R_sh}\frac{ab}{a+b}$$
したがってρcも求まります
$$ρ_c=L_s^2\times R_sh$$
TLM法を行う上での注意
これまで紹介したようにTLM法を用いることでチャネル材料の抵抗率、固有接触抵抗を求めることが可能ですが、うまく測定できない場合がありますのでうまくいかない場合は下記を意識してみてください。
TLMのパターンの寸法は本当に正しいか?
→測定していてIVがばらつきうまく直線に乗らないことがあります。そういった際はリフトオフ後のメタルの寸法が実際に予定していた通りになっているか確認してみてください。
IV測定は4端子法で測定しているか?
→チャネル抵抗率が小さい時は、2端子のIV測定では内部抵抗の影響で、うまく測りたい抵抗を算出することが出来ません。この場合は4端子法を用いることで内部抵抗の影響を無視して測定することが出来ます。
以上TLM法の解説でした。「チャネルの抵抗率を求めたい」「電極/半導体界面のコンタクト抵抗を求めたい」、そんな場合に役立つ方法になっています。是非今後活用してみてください。



コメント