今回はようやくキャリア密度の導出を行っていきます。
キャリア密度の導出は定期試験や大学院入試でも頻出だと思うので是非頑張って理解してみてください!
そもそもキャリア密度とは
キャリア密度は半導体中に存在する電流のもとであるキャリア(電子や正孔)の密度のことです。
つまりキャリア密度が高いと電気を良く運ぶことが出来ます。電気伝導の特性を担う重要なキャリア密度を今回根本から理解するために式を交えながら説明していきます。
キャリア密度を求めるには!?
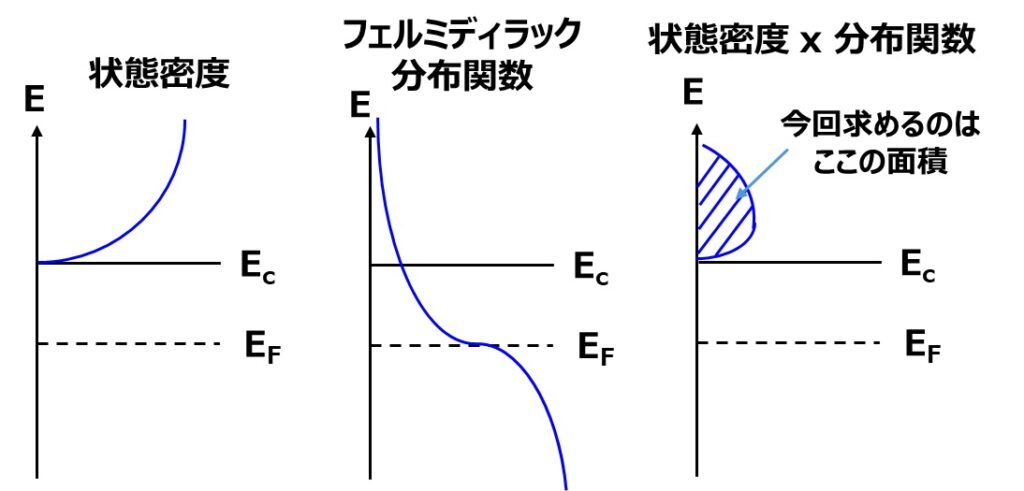
キャリア密度は状態密度とフェルミディラック分布の掛け算の積分で表されます。
状態密度とフェルミディラック分布関数は以下の記事を参照してみてください!
電子のキャリア密度の場合
実際に電子密度を求めてみます。
$$n(キャリア密度)=\int_{Ec}^{\infty}N_c(E)f_e(E)dE$$
で求めることが出来ます。
$$n(キャリア密度)=\frac{1}{2π^2}(\frac{2m_e}{ħ^2})^\frac{3}{2}(E-E_c)^\frac{1}{2}\frac{1}{1+exp(\frac{E-E_F}{kT})}dE$$
この計算をするにあたってフェルミディラック分布関数を以下のように近似します。
$$f_e(E)=\frac{1}{1+exp(\frac{E-E_F}{kT})}≒exp(-\frac{E-E_F}{kT})$$
よって先ほどの式は
$$n=\frac{1}{2π^2}(\frac{2m_e}{ħ})^\frac{3}{2}(E-E_c)^\frac{1}{2}exp(-\frac{E-E_F}{kT})$$
という風になります。
手を動かして計算をしてみると、
$$n=2(\frac{2πm_ekT}{h^2})^\frac{3}{2}exp(-\frac{E_C-E_F}{kT})$$
となります!
$$N_C=2(\frac{2πm_ekT}{h^2})^\frac{3}{2}$$
とすることで
$$n=N_Cexp(-\frac{E_C-E_F}{kT})$$
と計算できます。
$$N_C: 有効状態密度$$
と名付けられている定数を導入したわけですが、このNcは伝導帯の電子密度を表しています。
より細かく言うと伝導帯のキャリア密度が圧縮されている状態です。
正孔のキャリア密度の場合
価電子帯の正孔密度も同様に求めてみます。
$$p(キャリア密度)=\int_{Ev}^{-\infty}N_c(E)f_p(E)dE$$
計算すると
$$p=N_vexp(\frac{E_v-E_F}{kT}$$
$$N_v=2(\frac{2πmKT}{h^2})^\frac{3}{2}$$
Nvは価電子帯の正孔密度を表しています。有効状態密度になります。
有効状態密度の温度依存性
$$N_v=2(\frac{2πm_hKT}{h^2})^\frac{3}{2}$$
$$N_C=2(\frac{2πm_ekT}{h^2})^\frac{3}{2}$$
はそれぞれ温度によって値が変化することが分かります。
$$T^\frac{3}{2}$$
に対応して変化していきますので、実は温度に依存している変数であることに注意してください。
真性半導体とは?
真性半導体は不純物を含まない半導体のことです。つまり真性半導体は電子と正孔の数が同じ半導体になります。不純物を含まないため0 Kの状態ではキャリアは一つもありません。温度を上げると電子と正孔が一緒に対生成する為、同じ数になります。
つまりn=p=niです。
先ほどの式を代入いてみると
$$n_i=N_Cexp(-\frac{E_C-E_F}{kT})=N_vexp(\frac{E_v-E_F}{kT}$$
$$N_Cexp(\frac{2E_F}{kT})=N_vexp(\frac{E_c+E_v}{kT}$$
この等式を√をとりましょう。
$$\sqrt{N_C}exp(\frac{E_F}{2kT})=\sqrt{N_v}exp(\frac{E_c+E_v}{2kT}$$
これを用いて
$$n_i=\sqrt{N_C・N_V}exp(-\frac{-E_C+E_V}{kT})=\sqrt{N_C・N_V}exp(-\frac{-Eg}{2kT})$$
この状態でT=300[K]の時を考えます。すると
$$n_i≒1.5 \times 10^{16}$$
となります。
改めて
$$n_i=\sqrt{N_C・N_V}exp(-\frac{-Eg}{2kT})$$
この式を見ると
$$n_i 真性半導体のキャリア密度$$
は温度とバンドギャップに大きく依存しています。
特にバンドギャップの小さい半導体は温度に対する変化が大きいため、Ge(0.67eV)などは温度変化に対して敏感に反応します。
$$n_i^2=n \times p=N_C \times N_V exp(-\frac{-Eg}{kT})$$
なのでnpの積はバンドギャップにのみ依存しておりフェルミ準位には依存していないことが分かります。
つまりpnの積が一定という事実は不純物の入った半導体(p型やn型)でも同様に当てはめることが出来ます。
真性半導体のフェルミ準位を求める
真性半導体のフェルミ準位Eiを求めていきましょう。
$$n=p$$
なので先ほど同様
$$n_i=N_Cexp(-\frac{E_C-E_F}{kT})=N_vexp(\frac{E_v-E_F}{kT}$$
を考えます。
$$N_v=2(\frac{2πm_hKT}{h^2})^\frac{3}{2}$$
$$N_C=2(\frac{2πm_ekT}{h^2})^\frac{3}{2}$$
この時
$$m_e≒m_h$$
とすると
$$E_F(E_i)=\frac{E_c+E_v}{2}$$
となりフェルミレベルは伝導体と価電子帯のちょうど真ん中に位置することが分かります。





コメント