半導体工学の勉強やデバイスの研究をしている方はこの言葉をよく聞くと思います。
今回は金属/半導体の接続に関して取り扱っていきたいと思います。
ショットキー接続とオーミック接続とは何なのでしょうか?
「オームの法則」はV=I x R という公式でしたね。
これは電圧は電流に比例して一定の割合で増加していくという法則でした。
オーミック接続はこのオームから来ています。つまりV=I x Rが成り立つ接続です。
ショットキー接続は成り立たない整流性を持ってしまう接続になります。
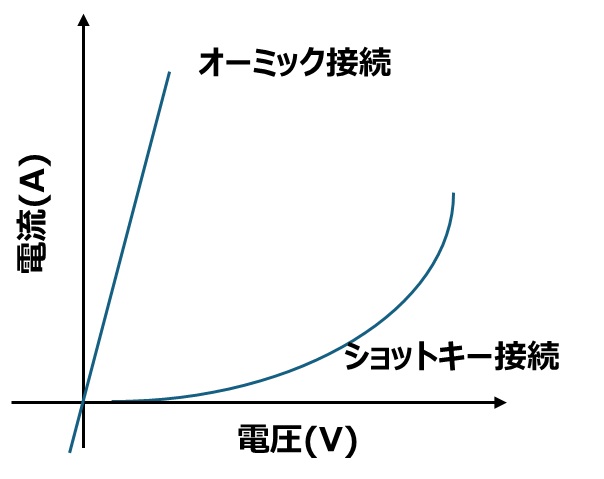
具体的には以下のようにオーミック接続がしっかりとれている場合VI特性は直線でショットキー接続の場合は曲線になります。
ショットキー接続・オーミック接続バンド図の書き方
例えば仕事関数φm, 電子親和力χsの金属と電子親和力φs, 電子親和力χsの半導体の接続を考えます。
接触していない時このような位置関係になりますが、接触するとフェルミ準位が一致するように界面からキャリアの拡散が生じます。
この時バンド図を書くと半導体側のバンド図はpn接合やMOS構造の時のようにバンドが曲がります。
この時のバンド構造は接合する材料の仕事関数の大小関係で決定します。
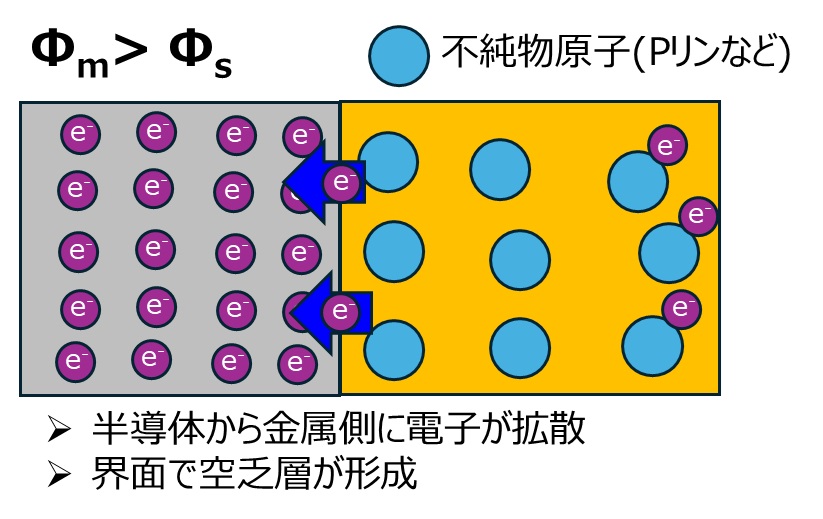
φm>φsの時
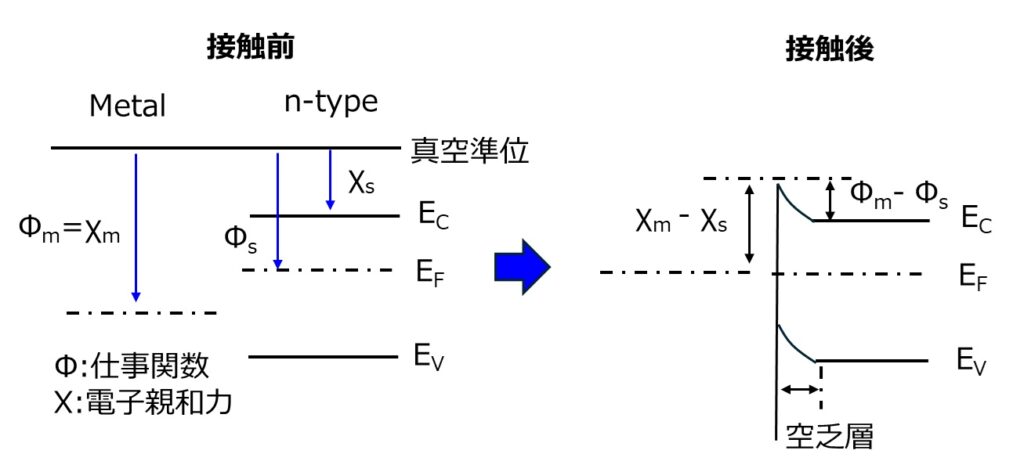
φs>φmの時
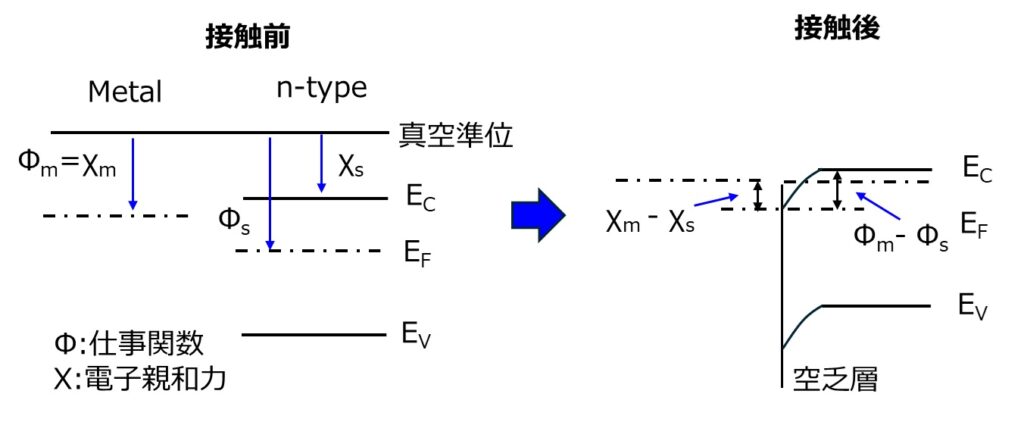
のようになります。
バンドの曲がりの定性的な説明
界面で異なる材料がくっついた時にフェルミエネルギーにギャップがあるとどうなるでしょう?
フェルミエネルギーはキャリアのエネルギー中間地点なので異種材料がくっついた時に、フェルミエネルギーが高い材料からフェルミエネルギーが低い材料にキャリアが拡散していきます。
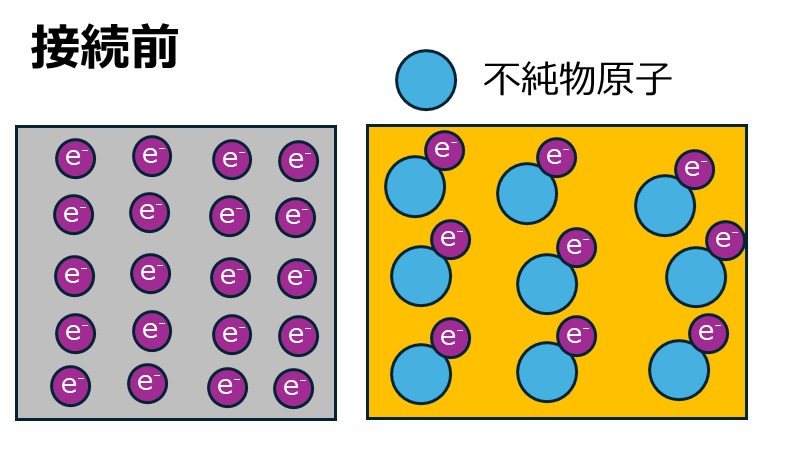
例えば仕事の関数の大きい金属と小さい半導体(n型)をくっつけた時にフェルミエネルギーは半導体側が大きいのでキャリアの電子が半導体から金属側に入ります。この時半導体との界面の電荷はつりあうので正電荷が生成されます。ここで生成された正の電荷により空乏層が生成されます。この時の電荷の空間分布がバンド図にも反映されています。
一方仕事関数の小さい金属を考えた時、このように金属側から電子が流れるのでこのように界面から半導体側に電子が流れ込みます。界面付近では電子がたくさん入り込んでドープされるので高濃度の電子添加がされた層がつくられて価電子帯がフェルミエネルギーに近づきます。
半導体の極性と接続性の関係
以上までの話をもとに半導体の持つ極性(pかnか?)が接続性に及ぼす関係をまとめました。

になります
実際に接続を考えるときには例えばデバイスの電極工程で考慮します。
以上接続の解説でした。


