シュレディンガー方程式とは?
時間を含まないシュレディンガー方程式は特に
$$ -\frac{ℏ^2}{2m}\frac{∂^2ψ}{∂x^2}+(V(x))-E)ψ=0 $$
という形で表されます。
ここで
$$ℏ:ディラック定数 m:粒子の質量 V:粒子の持つポテンシャルエネルギー$$
です
詳しくは別の機会にご紹介する予定ですが、ざっくりと説明すると電子を扱うために必要な方程式と考えてください。
古典力学では運動方程式で物体の動きを扱いましたが、半導体内で運動する物体は電子です。
電子は粒子性をもちろん持ってはいますが、波動性を持っていることも依然ご紹介しました。
しかし式を見て分かるように、この式を計算するとψという記号が求まります。
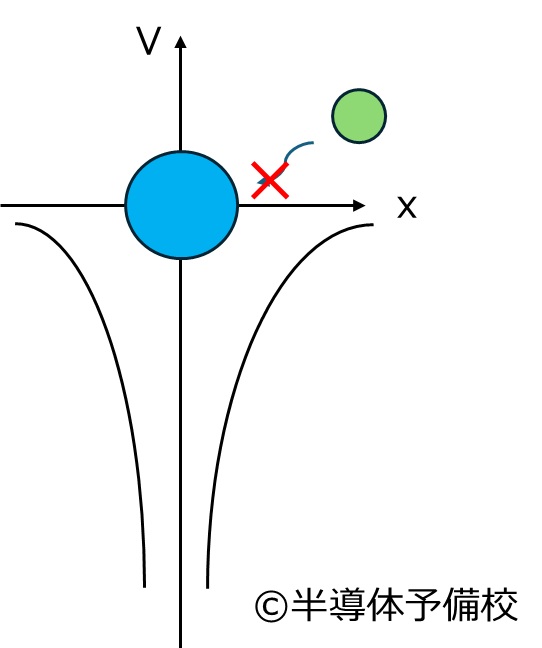
ψは「波の存在確立」言い換えると電子が存在する確率分布になります。
つまり上の絵のように電子の位置は条件の中で一意には決まらず存在できる位置をとびとびに移動していると解釈できます。
そしてもし決まった空間などに電子があれば、その空間内の各位置での電子の存在確立をすべて足し合わせると1になります。
$$\int_{0}^{V}(ψ(x)*ψ(x))dxdydz=1$$
これは規格化といい有限な領域の電子の存在を考えるときにかなり重要な考えかたになってきます。
具体例:1次元の箱に閉じ込められた電子の場合
以下の図のような場合を考えてみましょう。
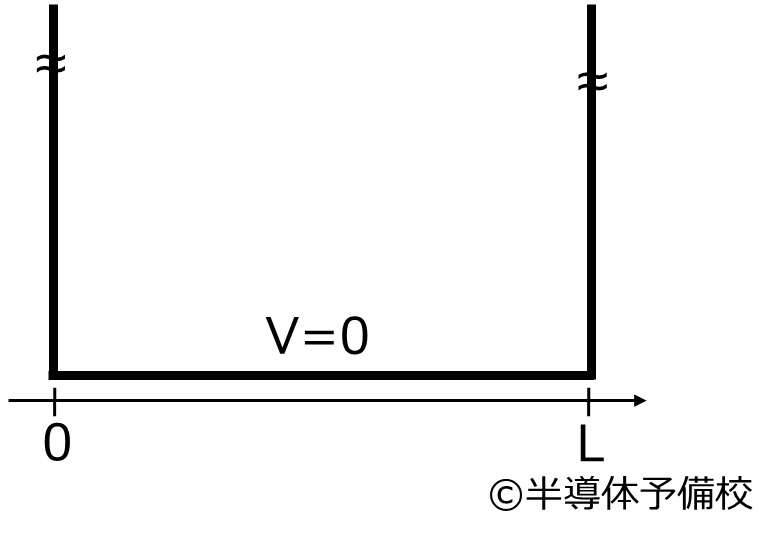
無限に高いとても堅い壁(ここではあえて分かりやすいようにこう表現しています)に囲まれた粒子が一つあるとします。
$$ -\frac{ℏ^2}{2m}\frac{∂^2ψ}{∂x^2}+(V(x))-E)ψ=0 $$
先ほどの式を考えましょう。箱の中のポテンシャルエネルギーは一定であるのでV=0にしても問題ありません。
1.V=0を代入して解を仮定する
先ほどの式にV=0を代入してみましょう。
$$ -\frac{ℏ^2}{2m}\frac{∂^2ψ}{∂x^2}-Eψ=0 $$
ここで微分方程式を考えます。上の式は微分方程式なので解を仮定して計算することで求めることが出来ます。
$$ψ=Aexp(jkx)+Bexp(-jkx)$$
と置いてみましょう。
この仮定した解を実際に代入して計算してみると
$$k^2=\frac{2m}{ℏ^2}E$$
が求まります。
ここまでできていますか??
2.境界条件を確認する。
冒頭で、無限に高い壁を仮定しました。これは壁に当たる部分で高いエネルギー的なポテンシャルの壁が存在していることを意味しています。つまりそこには電子が存在することはできません。
具体的に言うと例えば二つの電子の反発力は距離が近くなるほど大きくなりますね。例えばこの壁に電子に値するようなものがあればその位置に電子が存在することはありません。
そこで境界条件は
x=0の点とx=Lの点で電子の存在確立は0ということです。
条件として書くと以下のようになります。
$$x=0でψ(0)=0, x=Lでψ(L)=0$$
$$ψ(x)=Aexp(jkx)+Bexp(-jkx)$$
に実際代入して計算してみましょう
すするとA=-Bという事実が導くことが出来ます。
従って
$$ψ(x)=A(exp(jkx)-exp(-jkx))$$
になりますね。これをオイラーの公式を用いてsinの形に変形してみてください。
そうすると$$ψ(x)=2jAsinkx$$求められます。
簡単のために$$ψ(x)=Csinkx$$としてみましょう。
sinの中身に注目するとx=Lの時に0になるので
$$k=\frac{nπ}{L}$$
となります。
3.規格化を行う。
規格化をしてみましょう
$$1=int_{0}^{L}|ψ(x)^2|dx=int_{0}^{L}C^2sin^2(\frac{nπ}{L}x)dx=\frac{L}{2}C^2$$
になります。
よって
$$C=(\frac{2}{L})^{\frac{1}{2}}$$
です。
4.結果
この結果をまとめると
$$ψ(x)=(\frac{2}{L})^{\frac{1}{2}}sinkx$$
となります。
またエネルギーも求めてみましょう。
冒頭に導出した
$$k^2=\frac{2m}{ℏ^2}E$$
に
$$k=\frac{nπ}{L}$$
を導入してみましょう。すると
$$E_n=\frac{π^2ℏ^2}{2mL^2}・n^2$$
となります。
ここでnは自然数です。
なのでエネルギーはとびとびの値をとることが分かります。
これは箱の中で粒子はとびとびの席を確率的に移動しその席数によってエネルギーが離散的に決まってくることを意味しています。
これが何を意味するかというと、電子のエネルギーは連続的ではなく離散的にとるということを意味しています。


